第5章 三定数Wohl式によるPx,
xyデータの相関と熱力学解釈
5.1 三定数Wohl式の定義とその利点
2成分系において、三定数Wohl式は次式で与えられる。
lnγ1 = θ22 [A + 2(BC-A)θ1] (4-3)
lnγ2 = θ12 [B + 2(A/C-B)θ2] (4-4)
θ1 = Cx1/(Cx1 + x2) (4-5)
θ2 = 1 – θ1 (4-6)
ここで、γ1, γ2は軽質(低沸点)成分1と重質(高沸点)成分2の活量係数をそれぞれ表す。x1とx2は成分1と2のモル分率をそれぞれ表す。A,
BおよびCは定数である。すなわち、式(4-3)から式( 4-6)を用いて活量係数を計算し、定温Pxデータあるいはxyデータを相関する際には、組成x1が変化しても定数A, BおよびCはそれぞれ一定として扱う。
三定数Wohl式を用いると高温高圧の気液平衡データを精度よく相関できる。その例はFigure 4-2aおよび4-2bに示したhelium-4 (1) + nigrogen (2)系における定温Pxy関係に現われている。Figure 4-2bに示されるように、この2成分系ではxy関係が極大値をとっているにもかかわらず、液相は2相分離しない。このような単一液相維持系に対しても三定数Wohl式は精度よくxy関係を表すことができる利点がある。このときxy相関に用いた三定数(A, BおよびC)の値とは異なる三定数の値を用いることによってPx関係も精度よく相関できる。すなわち、三定数Wohl式を用いると、高温高圧気液平衡における単一液相維持系のPx, xy関係をそれぞれ精度よく相関できる利点がある。このとき、Px関係とxy関係はそれぞれ別個の三定数の組み合わせによって相関される。高温高圧気液平衡を二定数活量係数式によって精度よく相関することはできない。
低温気液平衡におけるPxデータに対して、2章で示したように、非共沸系はMargules式(二定数)によって精度よくPx関係を相関できる。また、それ以外の共沸系や2液相分離系についてはvan Laar式により精度よくPx関係を相関できる。低温気液平衡においては、2液相不分離単一液相維持系は存在しない。液相は2相に分離するから、Px関係から決定した二定数(相互作用パラメータ)をそのままxy関係の計算に用いることができる。この例外は、Figure 1-5に示した2-butanone (1) +
water (2)系であり、低沸点成分2-butanoneに富む液相組成範囲においてPx関係から決定した二変数を用いるxyの計算値とxyの実測値には明らかな差異が生ずる。二定数活量係数式の限界が現れている。低温気液平衡であっても、Pxデータから決定した二変数活量係数式を用いたxyの計算値と実測値に差異が生ずる場合には、三定数Wohl式をPxデータとxyデータに対して別個に適用するのが良い。文献に現われているように(Prausnitz J. M., [1, 5])、三定数活量係数式を低温気液平衡に適用すると実験誤差のために意味のある三定数を定められない。しかし、Pxデータから決定した二変数活量係数式を用いたxyの計算値と実測値に差異が生ずる場合には三定数活量係数式は意味をもつ。以下の解析では定温データのみ扱う。定圧データの扱い方は次の章で示す。
5.2 Pxデータ点と xyデータ点の信頼性判定
Pxデータ点については、次式を満たすときに信頼できる。
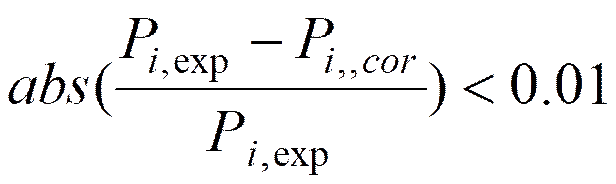 (5-1)
(5-1)
ここで、Pi,expは第i番目の全圧の実測値、Pi,corは相関式から計算した同じ組成における全圧の計算値である。
xyデータ点については、次式を満たすときに信頼できる。
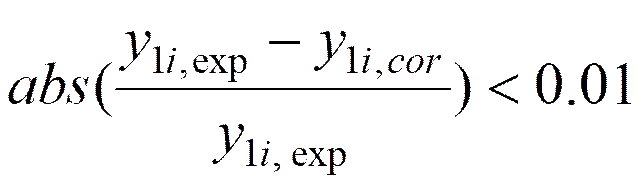 (5-2)
(5-2)
ここで、y1i,expは第i番目にある成分1の気相モル分率実測値、y1i,corは相関式から計算した同じ組成における成分1の気相モル分率計算値である。
5.3 定数Aの信頼判定
同一2成分系において、異なる温度に対するAの値は次の線形式によって相関できる。
![]() (5-3)
(5-3)
Tr1,iは第i番目の温度Tiにおける軽質成分1の還元温度(= Ti/TC1)である。TC1は成分1の臨界温度である。実測データが次の条件を満たすとき、Aのi番目の実測値Ai,expは信頼できる。
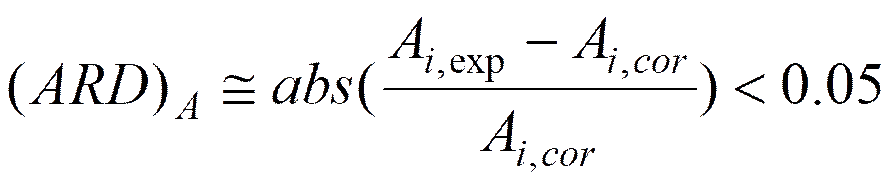 (5-4)
(5-4)
ここで、Ai,corは式(5-3)から計算される値である。すなわち、異なる温度に対するPxデータから決定される三定数A, B, Cのうち、Aは相対誤差が5%未満であれば信頼できる、xyデータから決定されるAについても同様である。
5.4 定数Aと温度の関係
Figure
5-1にhelium-4 (1) + nitrogen (2) 系に対するPxデータ9点のうち、式(5-4)を満たすデータ8点を示す、また、xyデータ8点も示す。x軸はTr1, y軸はAの値である。Figure
5-1から、PxデータもxyデータもTr1 vs. A の関係は良い直線性を示すことがわかる。また、温度が高くなるほど両直線の隔たりは大きくなる。また、xyデータから計算されるAの値はPxデータのそれより小さく、実測範囲外(Tr1
= 10)において両者は一致する傾向を示す。
Figure 5-2にhelium-4
(1) + nitrogen (2) 系に対するPxデータ9点のうち、式(5-4)を満たすデータ8点を示す、また、xyデータ8点も示す。x軸は1/Tr1, y軸はAの値である。Figure 5-2から、Pxデータもxyデータも1/Tr1 vs. A の関係は直線関係にならないことがわかる。この明瞭な差異は低沸点VLEデータにおいては現れない。その差異が実験誤差に紛れてしまうからである。
Figure
5-3にnitrogen (1) + methane (2) 系に対するPxデータ25点のうち、式(5-4)を満たすデータ13点を示す、また、xyデータ13点も示す。x軸はTr1, y軸はAの値である。Figure
5-3から、PxデータもxyデータもTr1 vs. A の関係は良い直線性を示すことがわかる。Figure 5-4にnitrogen
(1) + methane (2) 系に対するPxデータ25点のうち、式(5-4)を満たすデータ13点を示す、また、xyデータ13点も示す。x軸は1/Tr1, y軸はAの値である。Figure 5-4から、Pxデータもxyデータも1/Tr1 vs. A の関係は直線関係にならないことがわかる。
Figure 5-5にcarbon
dioxide (1) + butane (2) 系に対するTr1 対Aの関係、
Figure 5-6にmethanol
(1) + water (2) 系に対するTr1 対Aの関係、
Figure 5-7にhydrogen
(1) + methane (2) 系に対するTr1 対Aの関係、
Figure
5-8に argon (1) + methane (2) 系に対するTr1 対Aの関係、
Figure
5-9に argon (1) + ammonium (2) 系に対するTr1 対Aの関係、
Figure
5-10にmethane (1) + ethylene (2) 系に対するTr1 対Aの関係、
Figure
5-11にethylene (1) + ethane (2) 系に対するTr1 対Aの関係、
Figure
5-12にcarbon dioxide (1) + propane (2) 系に対するTr1 対Aの関係、
Figure
5-13にcarbon dioxide (1) + methanol (2) 系に対するTr1 対Aの関係、
Figure
5-14にcarbon dioxide (1) + water (2) 系に対するTr1 対Aの関係、
Figure
5-15に propylene (1) + propane (2) 系に対するTr1 対Aの関係、
Figure
5-16に ammonium (1) + water (2) 系に対するTr1 対Aの関係、
Figure
5-17 に1-butene (1) + butane (2)系に対するTr1 対Aの関係、
Figure
5-18に benzene (1) + heptane (2) 系に対するTr1 対Aの関係
を示す。これらの図からTr1 対Aの関係は良い直線性を示すことがわかる。温度が第一成分の臨界温度TC1を下回るとPxデータから決定されるAの値にxyデータから決定されるAの値は近づくが、Figure 5-11に示すethylene (1) + ethane (2)系では、両者は明瞭な差異を示している。これらの知見は、超臨界領域にある気液平衡データに対して仮想液体の蒸気圧を割り当て、かつ、三定数Wohl式を用いて相関したことにより得られた結果である。
5.5 定数Cの温度に対する関係とTCラインによる相関
次式によって定義されるCTCを臨界点到達率Xに対してプロットすることにより、定数Cと温度の収束関係が得られる。
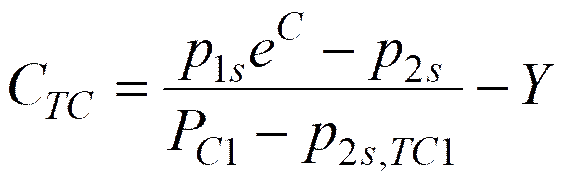 (5-5)
(5-5)
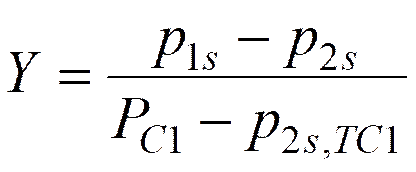 (5-6)
(5-6)
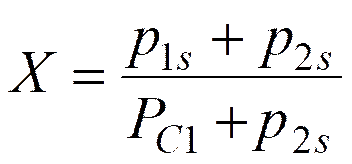 (5-7)
(5-7)
ここで、p1s,
p2sおよびPC1は成分1と2の蒸気圧および成分1の臨界圧をそれぞれ表す。P2s,TC1は成分1の臨界温度における成分2の蒸気圧である。その収束関係は次のTCライン(Thermodynamic
Consistency Line)によって簡単な関数として表すことができる。
![]() (5-8)
(5-8)
![]() (5-9)
(5-9)
![]() (5-10)
(5-10)
ここでaおよびbは相関定数である。低温気液平衡データの解析においては式(5-8)あるいは式(5-9)を用いることができる。高温気液平衡データの解析には式(5-10)を用いることができる。YとXの関係はXの広い範囲で累乗関係にあるので、この関係の上にCと温度の関係を展開するのである。
低温気液平衡Pxデータは、非共沸混合物に対しては二定数Margules式を、その他の共沸混合物あるいは2液相形成系については二定数van Laar式を用いて相関できる。三定数Wohl式を適用するためには、先ず、次の二定数NRTL式をMargules式あるいはvan Laar式から計算されるPx関係に一致させる。あるいは、Margules式、van
Laar式から計算される無限希釈活量係数, lnγ1∞とlnγ2∞に一致するようにNRTL式の二定数を決定する。その後に、二定数NRTL式から計算されるPx関係に三定数Wohl式を一致させる。三定数Wohl式においてC = 1、あるいは、C = A/Bに特定すると、それぞれ、二定数Margules式、および、二定数van Laar式に一致する。そこで、二定数NRTL式を介在させて三定数Wohl式の定数A, B, Cを決定するのである。このとき、A =
lnγ1∞、および、B = lnγ2∞の両方が満たされている。二定数NRTL式は次のように与えられる。
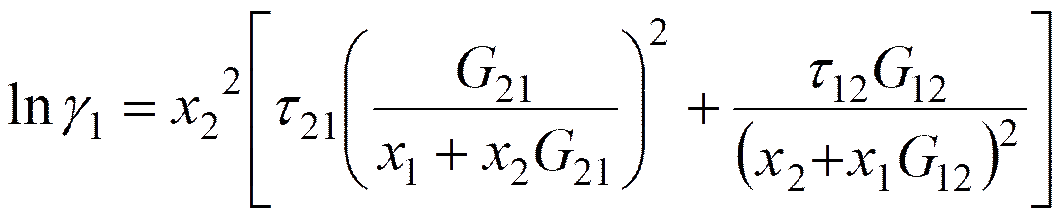 (5-11)
(5-11)
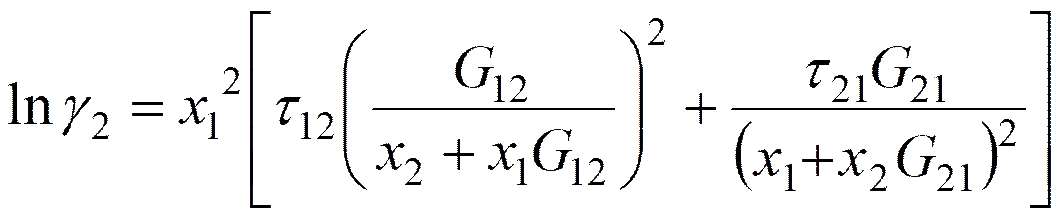 (5-12)
(5-12)
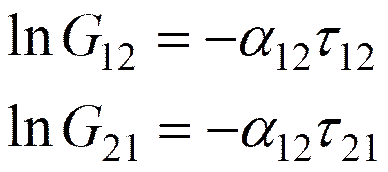 (5-13)
(5-13)
ここでα12は0.3に固定される。
Figure 5-19にethanol (1) + water
(2)系に対するCTCをXに対して示す。CTCはXに対して式(5-8)で表される直線関係にあることが分かる。
Figure
5-20に2-butanone (1) + water (2)系、
Figure 5-21にethanol (1) +
2,2,4-trimethylpentan (2)系、
Figure 5-22にwater (1) +
furfural (2)系、
Figure 5-23にcyclohexane (1) +
aniline (2)系、
についてCTCとXの関係示す。先の2つの系に対するTCラインとして式(5-8)が、また、後の2つの系に対しては式(5-9)が適用できる。
Figure 5-24からFigure 5-28にこれらの系に対するCとTr1の関係を示す。青色実線はTCラインと式(5-5)から求めたCの値を示している。三定数Wohl式と実測値から決定したCの値の平均値と一致している。すなわち、TCラインを用いると精度よくCと温度の関係を決定することができる。これらの図にはAとTr1の関係も示した。定温データであるから、式(5-4)を満たさないデータの判定は行っていない。Figure 5-24からFigure 5-28は、AとTr1は直線関係にあることを示している。
5.6 定数Bと温度の関係
定数Bは温度と線形関係にある。Figure
5-24からFigure 5-28にBとTr1の関係を示す。AとTr1の関係と比べるとBとTr1の関係は実験誤差が大きく現れる。
5.7無限希釈部分モル過剰エンタルピーとエントロピーの補償関係
軽質成分1の無限希釈部分モル過剰エンタルピーh1∞とエントロピーs1∞は次式によって定義される
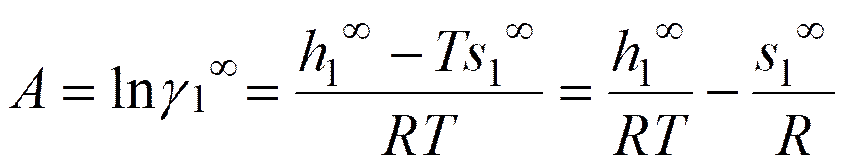 (5-14)
(5-14)
Rは気体定数である。成分2の無限希釈部分モル過剰エンタルピーh2∞とエントロピーs2∞も定数Bを用いて同様に定義される。実験データからh1∞とs1∞を決定するには、Aと1/Tの関係を線形と仮定して勾配からh1∞を、切片からs1∞を決定する。Figure 5-29に低沸点VLEデータから計算したh1∞/298.15Rとs1∞/Rの関係を、また、h2∞/298.15Rとs2∞/Rの関係を示す。さらに、高圧VLEデータから計算したこれらの値も示す。Figure 5-29は次のエントロピー・エンタルピー補償則が成立することを示している。
298.15si∞/hi∞ = 0.66 (5-15)
高圧データから決定する補償則に比べて低沸点データから決定する補償則は収束性が高い。実験データが式(5-15)から隔たる理由は各々の二成分系に固有な分子配置と分子間相互作用の関係があることによる。そのことは、ガスクロマトグラフィー測定によって軽質アルカン(1)
+ 重質アルカン(2)系では次の補償則が精度よく成り立つことが示されていることからもわかる(S.
Kato et al., Ind. Eng. Chem. Res. 2003 42 4927-4938).
298.15si∞/hi∞ = 1.8 (5-16)
三定数Wohl式を用いるVLEデータの相関は高圧データの相関を可能とするのみならず、エントロピー・エンタルピー補償則を明らかにすることができる利点がある。
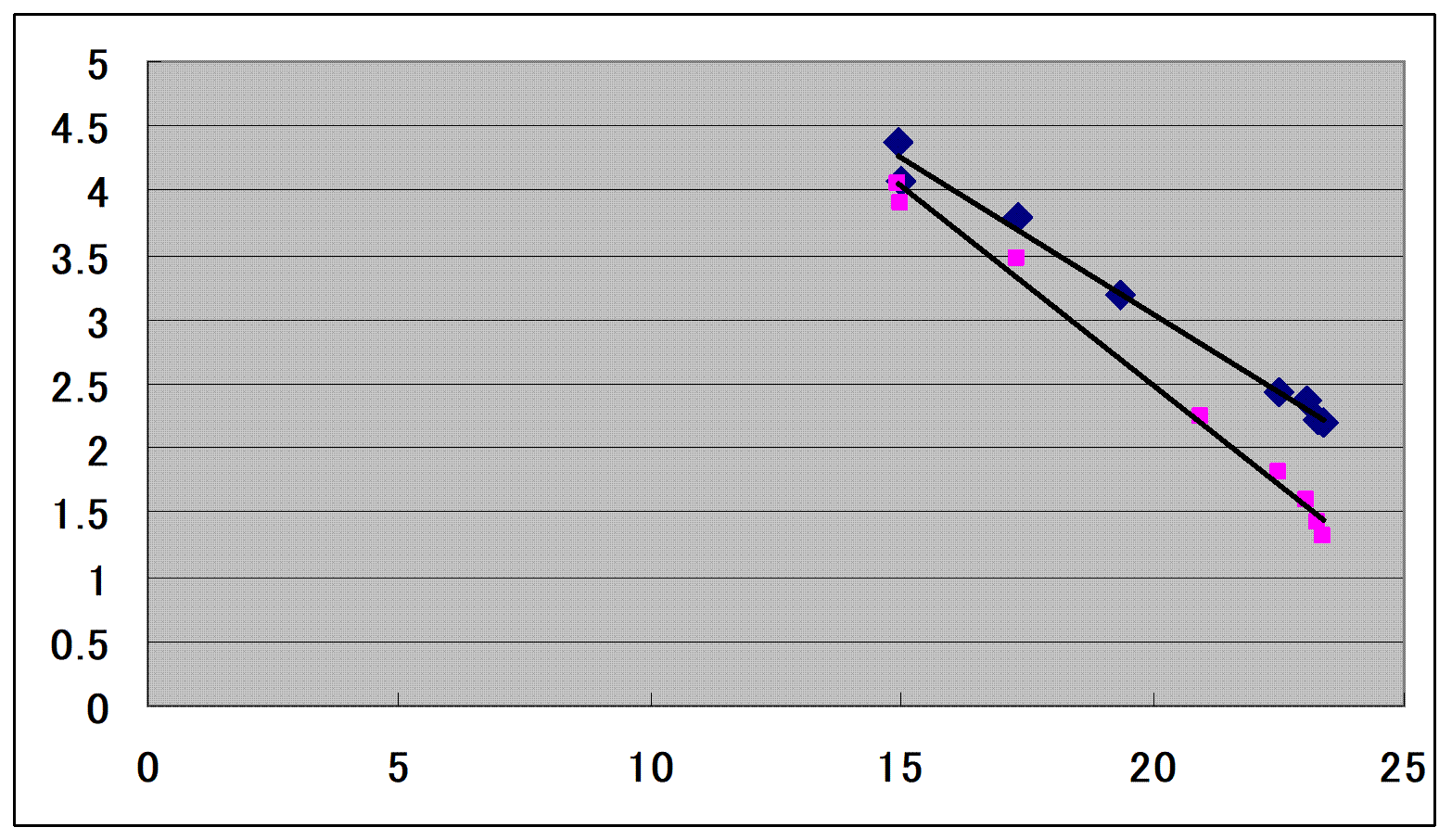
Figure
5-1. A vs. Tr1 for the helium-4 (1) + nitrogen (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
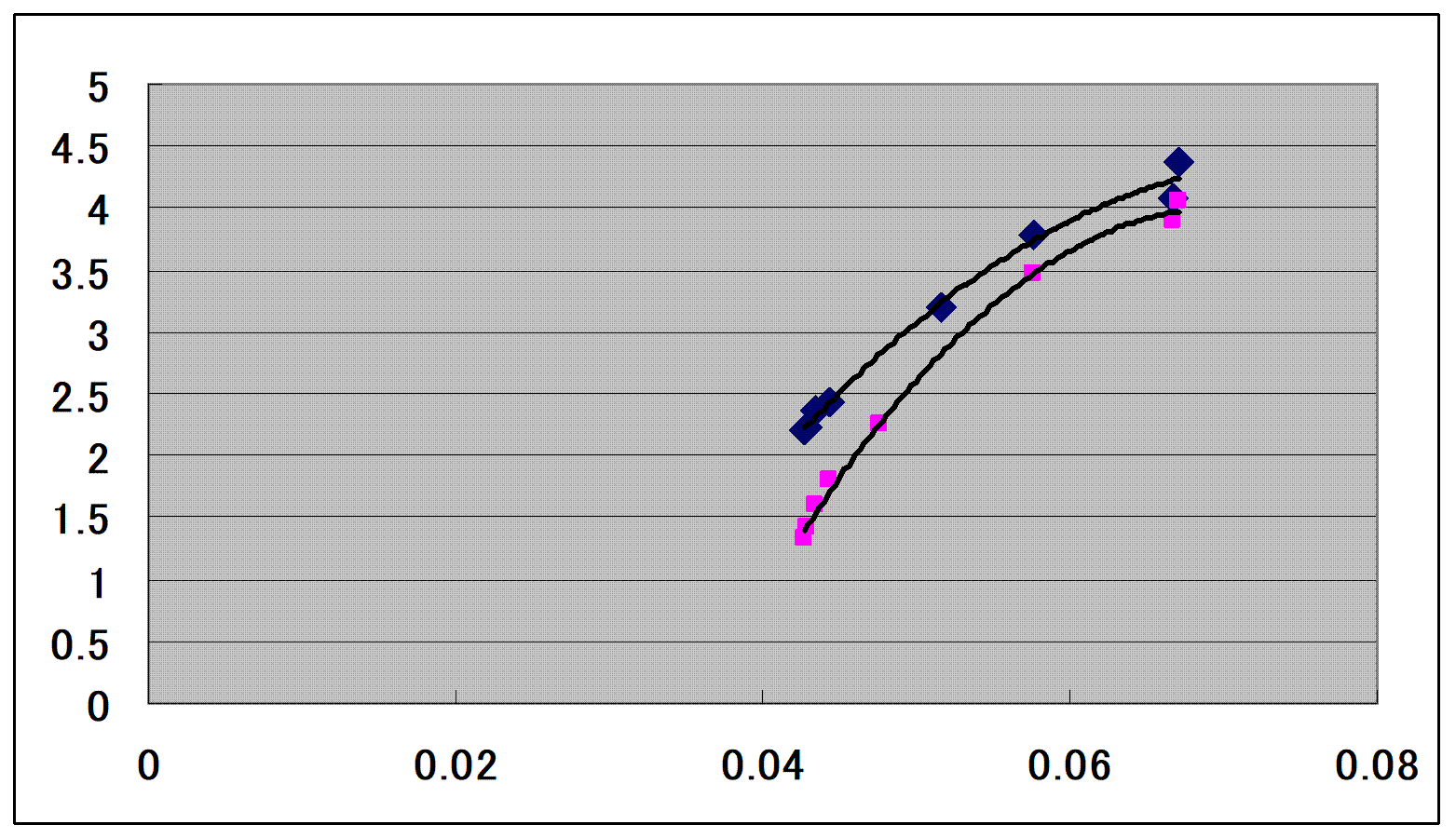
Figure
5-2. A vs. 1/Tr1 for the helium-4 (1) + nitrogen (2) system, x:-axis: 1/Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−) polynomial
correlations.
Figure
5-3. A vs. Tr1 for the nitrogen (1) + methane (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-4. A vs. 1/Tr1 for the nitrogen (1) + methane (2) system, x-axis: 1/Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−) polynomial
correlations.
Figure
5-5. A vs. Tr1 for the carbon dioxide (1) + butane (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-6. A vs. Tr1 for the methanol (1) + water (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [2,4], (●)
calculated using xy data [2,4], (−)
linear correlations using Eq. (5-3).
Figure
5-7. A vs. Tr1 for the hydrogen (1) + methane (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-8. A vs. Tr1 for the argon (1) + methane (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-9. A vs. Tr1 for the argon (1) + ammonium (2) system, x:-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-10. A vs. Tr1 for the methane (1) + ethylene (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-11. A vs. Tr1 for the ethylene (1) + ethane (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-12. A vs. Tr1 for the carbon dioxide (1) + propane (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-13. A vs. Tr1 for the carbon dioxide (1) + methanol (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-14. A vs. Tr1 for the carbon dioxide (1) + water (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-15. A vs. Tr1 for the propylene (1) + propane (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
1Figure
5-16. A vs. Tr1 for the ammonium (1) + water (2) system, x-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-17. A vs. Tr1 for the 1-butene (1) + butane
(2) system, x-axis:
Tr1 and y-axis: A, (●)
calculated using Px
data [4], (●)
calculated using xy data [4], (−)
linear correlations using Eq. (5-3).
Figure
5-18. A vs. Tr1 for the benzene (1) + heptane (2) system, x:-axis: Tr1 and y-axis: A, (●)
calculated using Px
data [2, 4], (●)
calculated using xy data [2, 4], (−)
linear correlations using Eq. (5-3).
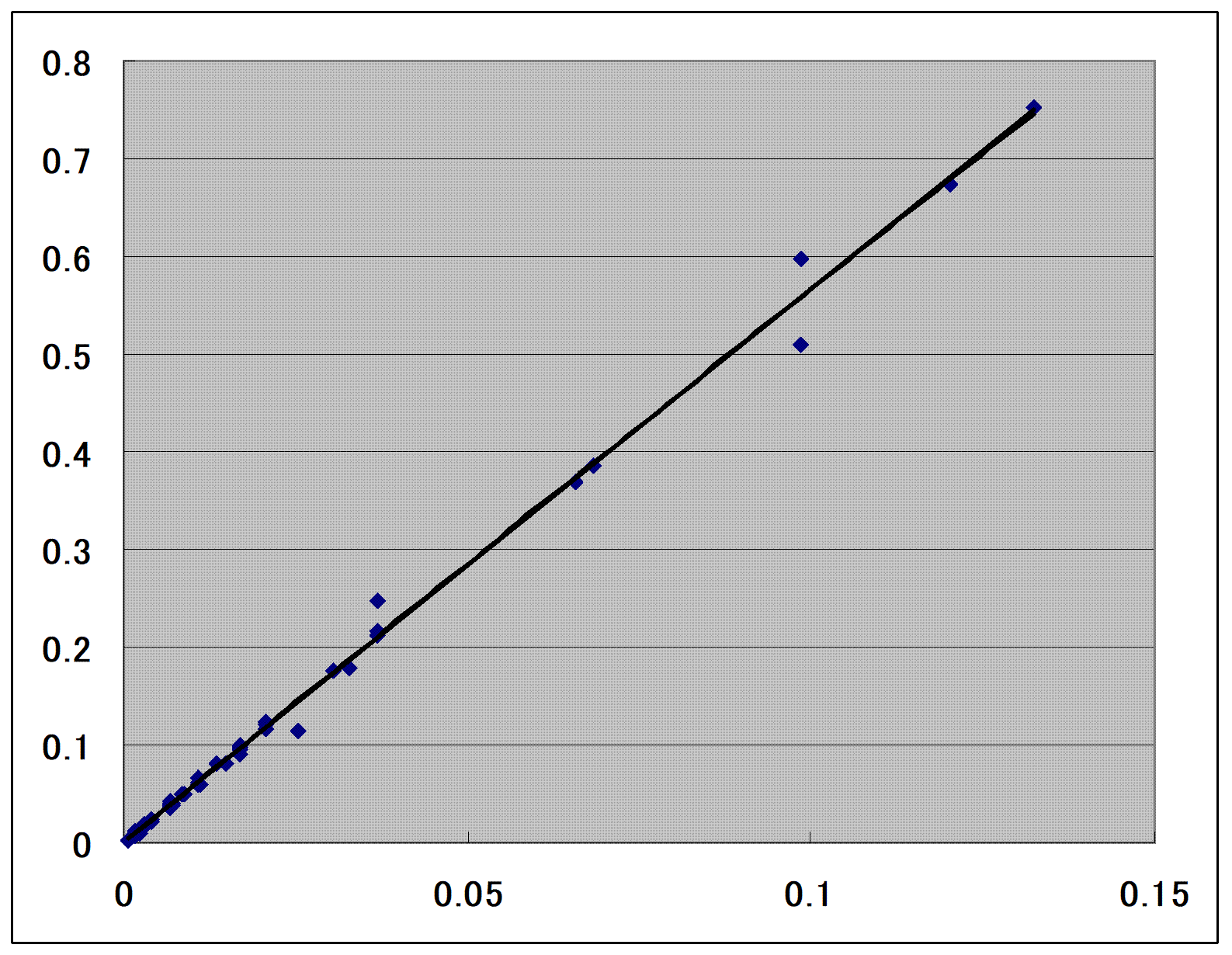
Figure
5-19. CTC vs. X for the ethanol (1) + water (2) system
calculated using Px
data, x-axis:
X and y-axis: CTC, (●)
experimental CTC data [2] and (−)
correlated using Eq. (5-8).
Figure
5-20. CTC vs. X for the 2-butanone
(1) + water (2) system calculated using Px data, x-axis: X and y-axis: CTC, (●)
experimental CTC data [2] and (−)
correlated using Eq. (5-8).
Figure
5-21. CTC vs. X for the ethanol
(1) + 2,2,4-trimethylpentan (2) system calculated using Px data, x-axis: X and y-axis: CTC, (●)
experimental CTC data [2] and (−)
correlated using Eq. (5-8).
Figure
5-22. CTC vs. X for the water
(1) + furfural (2) system calculated using Px data, x-axis: X and y-axis: CTC, (●)
experimental CTC data [2] and (−)
correlated using Eq. (5-9).
Figure
5-23. CTC vs. X for the cyclohexane
(1) + aniline (2) system calculated using Px data, x-axis: X and y-axis: CTC, (●)
experimental CTC data [2] and (−)
correlated using Eq. (5-9).
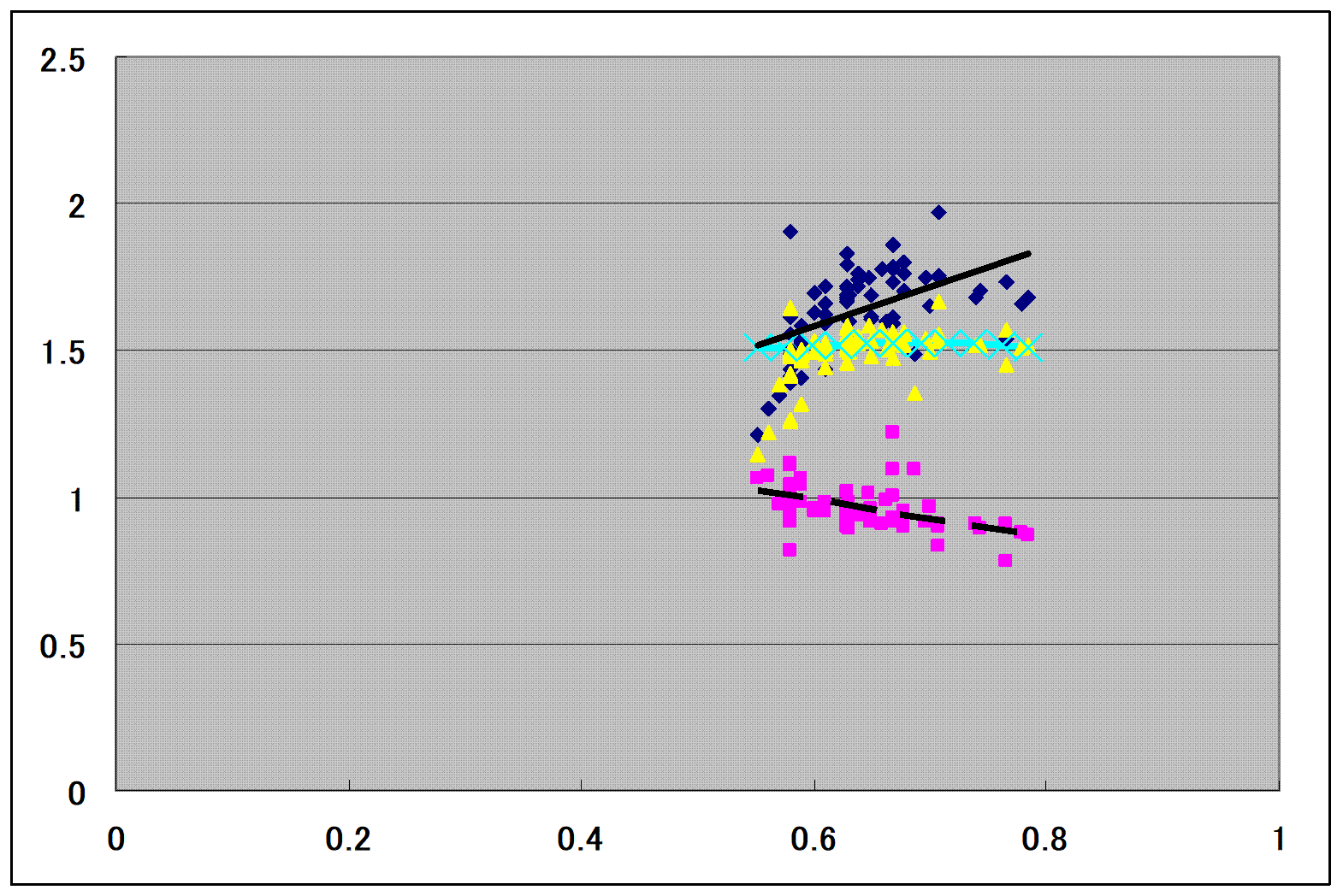
Figure
5-24. A, B and C
vs. Tr1 for the
ethanol (1) + water (2) system calculated using Px data [2], x-axis: Tr1 and y-axis:, A, B
and C , (●)
experimental A values, (●) experimental B values, (●)
experimental C values, (−) linear correlation
of the A values, (- - -) linear correlation of the B values and (−) C values predicted using Eq. (5-8).
Figure
5-25. A, B and C vs. Tr1 for the 2-butanone (1) + water (2) system calculated
using Px
data [2], x-axis:
Tr1 and y-axis:, A, B and C , (●)
experimental A values, (●) experimental B values, (●)
experimental C values, (−)
linear correlation of the A values,
(- - -) linear correlation of the B
values and (−) C values predicted using Eq. (5-8).
Figure
5-26. A, B and C vs. Tr1 for the ethanol (1) + 2,2,4-trimethylpentan (2)
system calculated using Px
data [2], x-axis:
Tr1 and y-axis:, A, B and C , (●)
experimental A values, (●) experimental B values, (●)
experimental C values, (−)
linear correlation of the A values,
(- - -) linear correlation of the B
values and (−) C values predicted using Eq. (5-8).
Figure
5-27. A, B and C vs. Tr1 for the water (1) + furfural (2) system calculated
using Px
data [2], x-axis:
Tr1 and y-axis:, A, B and C , (●)
experimental A values, (●) experimental B values, (●)
experimental C values, (−)
linear correlation of the A values,
(- - -) linear correlation of the B
values and (−) C values predicted using Eq. (5-9).
Figure
5-28. A, B and C vs. Tr1 for the cyclohexane (1) + aniline (2) system
calculated using Px
data [2], x-axis:
Tr1 and y-axis:, A, B and C , (●)
experimental A values, (●) experimental B values, (●)
experimental C values, (−)
linear correlation of the A values,
(- - -) linear correlation of the B
values and (−) C values predicted using Eq. (5-9).
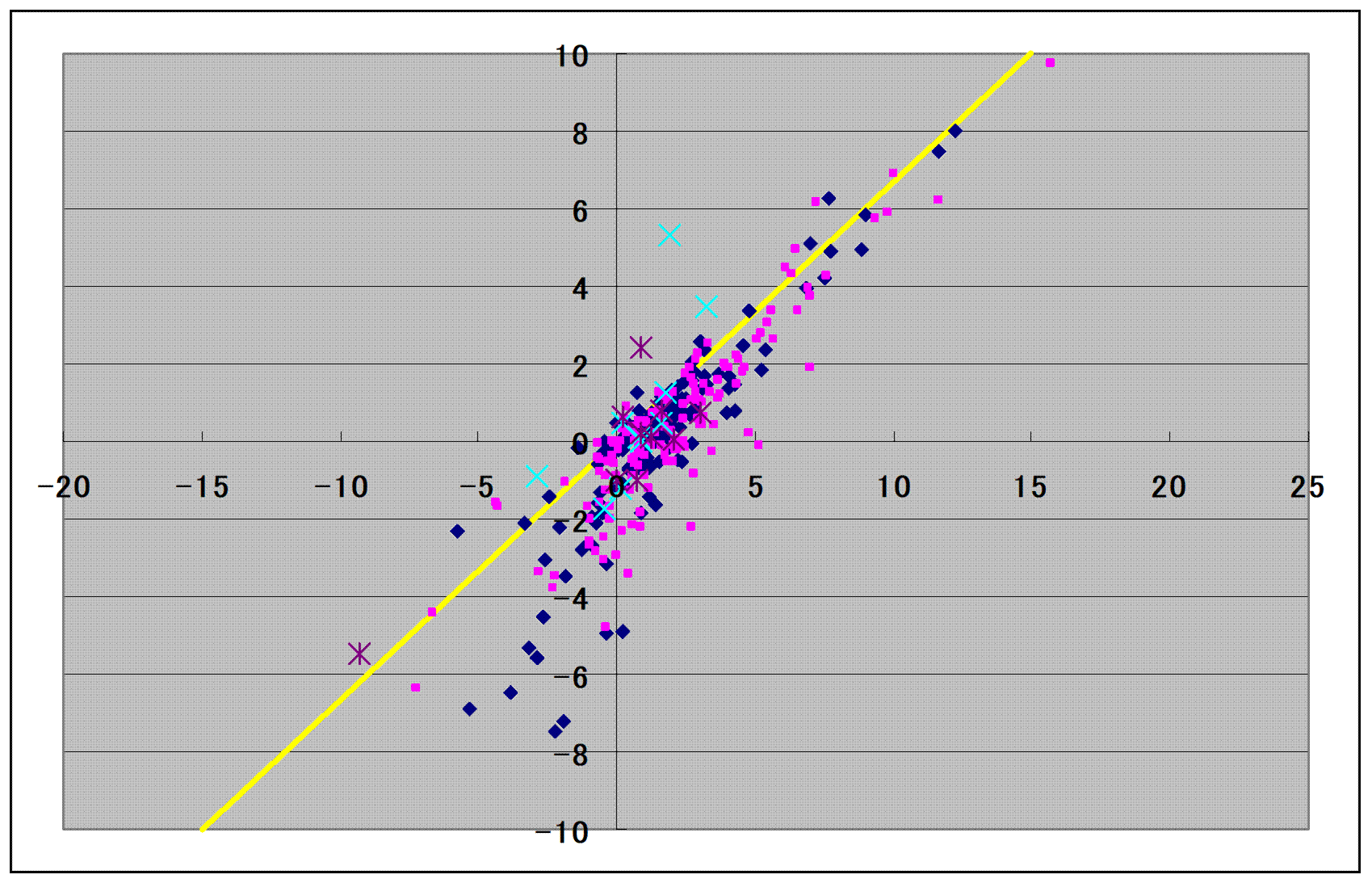
Figure 5-29. h1∞ vs. s1∞ and h2∞ vs. s2∞ for the low and high temperature A
and B values, x-axis: h1∞ and h2∞, y-axis: s1∞ and s2∞, (●) h1∞ vs. s1∞ using low
boiling point data [2, 3], (●) h2∞ vs. s2∞ using low boiling point data [2, 3], (×) h1∞ vs. s1∞ using high pressure data [4] and (×) h2∞ vs. s2∞ using high pressure data [4].